I just returned from the summer meeting of the Transportation Research Board’s AFB-80 committee. This is a standing committee that deals with high accuracy geospatial data acquisition for transportation applications. We always have a lot of very interesting presentations at this conference but seldom big surprises. This year was an exception when (gasp!) Dr. Michael Dennis of NGS announced that the US Survey foot will be deprecated when the new 2022 spatial reference system comes online. There was a bit of banter that, in the current political climate, we might have to rename the International Foot the “American Freedom Foot…” I pleaded that we just jump to the metric system but, sadly, that is not going to happen.
I often leave bits of unfinished business in my wake. Looking back on some previous Random Points columns, I noticed that justification for vertical “debiasing” of LIDAR data is one of those dangling items. I made a statement that, under certain circumstances, we can shift the vertical of a point cloud. Let’s make up a rule for this.
I have done a small amount of research on this topic (meaning I typed it in to Google) with no satisfying results. Thus I will just develop my own guidance on this and see what kind of complaints are forthcoming.
Figure 1: True View 410 Test Data Set
Consider the data set of Figure 1 flown at our test range (“The Shop”). This is a LIDAR data set from a GeoCue True View 410, colorized by the integral oblique cameras. The True View 410 uses a Quanergy M8 Ultra laser scanner. This is an 8-beam scanner with a total pulse repetition rate of 420 KHz. Note the check points set out over the test area. There are 21 total check points in this particular project. I have eliminated 4 of these. One is the base station and should always be eliminated since the tripod and antenna inject vertical “noise.” The other three were eliminated because the targets were missing. There are several others I would like to eliminate because it would make the statistics better. This brings us to the first rule of measuring accuracy; you cannot eliminate a check point from the data set without a justifiable reason. Bad accuracy is not one of those reasons! After eliminating the base and the three missing targets, I observe a Root Mean Square Error (RMSE) of 5.7 cm. This is actually quite good considering the fact that this is positioning without the introduction of ground control. The mean error is -5.0 cm and a total error range is 8.8 cm
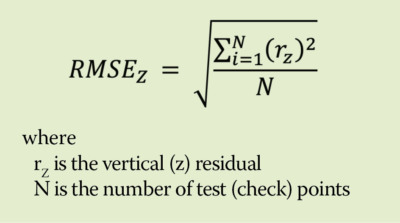Now recall from a 2017 Random Points column (I am inferring the “i” subscript for each point):
We do this square root of the residuals squared trick because we do not want negative residuals canceling positive ones. There is an incredibly important but sometimes neglected relationship between bias, mean error and variance that needs to be considered when thinking about error analysis:
In our data set, we could significantly improve the RMSE if we shifted all the data by the mean of -5.0 cm. This is frequently performed by LIDAR processing technicians and is popularly referred to as a “Z bump.” But is this a legitimate operation? My suggestion is that we use our idea of how certain we are of the mean to make this decision. This certainty can be obtained by examining the Standard Deviation of the Mean (SDOM):
I argue that if |r| ‒ SDOM > 0 then debiasing is legitimate. This is saying that if the uncertainty in the mean is small relative to the mean itself, we can shift the mean. For our example, the sample standard deviation is 2.74 cm (I get this by rearraigning the equation for RMSE). The number of check points that have been used, N, is 17. This gives an SDOM of 0.66 cm. This is well outside of our mean error of -5.0 cm so I can apply the “Z bump.” Once I shift the data (using a LAS shift tool in True View Evo or LP360) and recompute the residual error, I obtain the results of Figure 2.
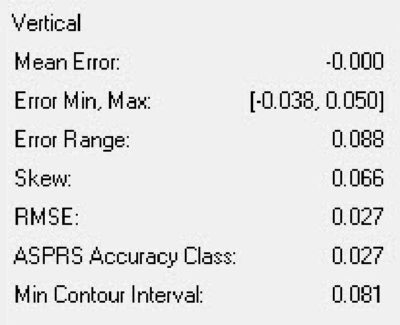
Figure 2: Error after “Z bump”
Note that, as expected, the new mean is zero. If it is not, then I made a mistake! The error range remains, of course, unchanged. But the new RMSE is now 2.7 cm. This has significantly improved the accuracy quality of these data, at least according to the way we measure accuracy using the new ASPRS accuracy specifications.
I think, until someone raises a mathematically sound objection, that the SDOM test is a justification for performing the Z bump. Now a physicist would say “This is a systematic error. You need to find the root cause of this error and correct it.” I consider myself a student of physics and completely agree with this stance. However, we often do not have enough information about the internals of the laser scanning systems we use to make this determination. I am sure others will argue that maybe we need to use 2 × SDOM or some other factor. That is a good debate to have.
I intend to write a more detailed white paper on this topic and publish to our web site. Till then, I think this is a start. This should make you feel better about doing the Z bump while your parents are watching.