OK, this article, in keeping with the column title, is truly a Random Point!
There has been a lot of talk lately about developing a new standard for point cloud data (mostly for LIDAR and dense image matching, DIM). The Open Geospatial Consortium (OGC) recently announced a position of supporting emerging and existing community standards rather than pursuing a standard of their own. This position was probably taken because point clouds have reached the level of maturity that no one standard will satisfy everyone. Other groups, meanwhile, are plowing ahead with a replacement for the ubiquitous LAS format. I personally am hoping something very clever emerges that still retains a few of the LAS features that have made the format so successful.
There is a lot wrong with LAS (just like there is a lot wrong with the de factor vector format, Shape) but a few things have stood the test of time. The first is the very simple idea of making LAS a rectangular cuboid container. This decision led to projects being naturally tiled, providing the first level of indexing for a rapid access data management system. I find it quite interesting that after 20 years of trying to develop point storage databases, the file-based rectangular cuboid dominates all main stream access systems. As far as I know, all very high-performance streaming display systems today are based on some variant of an octree which is, of course, a rectangular cuboid system.
The second thing we did right when developing the very first iteration of LAS was to make the point representation integers rather than floating point numbers. This was a very deliberate decision even though it poses some extra overhead on storage and retrieval. At the time of the original design, it was still common practice for anyone writing computer software to be well-versed in numerical analysis (something that I fear may be disappearing from modern curricula). A student of Hamming’s “Numerical Methods for Scientists and Engineers” (a book which is fully relevant to this day) knows the logarithmic resolution problem with floating point numbers in computers. The scaled and offset integers of LAS coordinates circumvent this problem. So now some thoughts on reinventing…
Some folks count sheep when they cannot sleep. I tend to try to do some sort of mathematical estimation problem (I know; very strange and it does more to keep you awake than to induce sleep). I was recently trying to estimate some relationships between weight and size which led me to think about the beauty of the original design (during the French Revolution) of the metric system. The core of the system was the unit of length, the meter (or metre if you are not in the USA!). In 1793 the meter was defined to be one ten-millionth the distance from the equator to the North Pole along a meridian passing, of course, through Paris. The impracticality of this was quickly realized and it was redefined in terms of a platinum reference bar (“mètre des Archives”) in 1799.
The definition of the meter was not the clever bit. The first good piece of thinking was to define all super and sub units as powers of ten (a decimal system)—none of this nonsense of 16 ounces to a pound, 12 inches to a foot and so forth. That makes it very easy to remember as well as to do quick estimates. One would think this as completely obvious but here in the good old USA we still use yards, feet and inches, none of which are rational relative to one another!
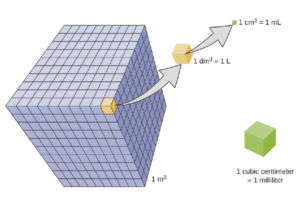
The really clever bit was to base the units of volume and weight on water and the meter. The kilogram was, by definition, the mass of a cube of water (the water being at standard pressure and the temperature of maximum density, about 4 C) where the cube was 1/10 of a meter on edge. This leads immediately to the Centimeter-Gram-Second (CGS) definition of a milliliter being the volume of a cube exactly 1 cm on edge and the gram being the mass of water that occupies that cube (see Figure 1). Even though, in the US system, a fluid ounce is approximately 1 ounce weight, the system falls apart when you hit cups, pints and pounds.
Because of this very clever original definition of the metric system, it is a piece of cake to make estimations in your head. All you need to remember is the density of whatever you are estimating. Of course, quite often it is water where the density is one (or certainly close enough for estimations). Want to know the mass of a 1 liter bottle of soda pop? Well, soda is essentially water so it’s 1 kilogram. We are keenly interested in estimating weight in aircraft systems when discussing fuel loads. Jet A-1 fuel has a density of about 800 grams per liter (actually 804 but the 800 number is good enough for estimations). If I load 1,000 liters of fuel, I have a mass of 800 kg. Estimating tank volumes in terms of liquid measure is direct; just compute the volume in cubic centimeters and you have the fluid volume in milliliters. At a deeper level, the metric system is a rationalized system of measure. Basically, this means that derived units such as those of energy and electromagnetism require no artificial constants in their defining equations. This is beautiful in its simplicity and lucidity.
So what does all this have to do with point cloud formats? Actually, nothing at all. My hope is simply that we can apply some of the exceptionally clever thought processes of the original design of the metric system to any new definition on which the industry embarks. It’s unlikely that any of the nice relations of powers of ten and deriving from the unit of length apply directly but the very rational thought process should most definitely be a guiding principal. Here’s to cubic thinking!!